1. 树分治
树分治是一种统计树上路径的方法。
例题:P2634 这道题要求我们统计树上长度为 3 的倍数的路径的个数。设 $(u,v)$ 表示 $u$ 到 $v$ 的路径。让我们先来考虑怎么统计满足 $lca(u,v) = i$ 的长度为 3 的倍数的路径个数。我们可以维护一个桶 $b$,$b_j$ 表示 $i$ 到子树内的点的路径中,有多少个长度模 3 为 $j$。依次遍历 $i$ 的每个子树。假设现在枚举的子树以 $x$ 为根,找到 $x$ 子树中每个点到 $i$ 的路径的长度,然后用桶算一下就可以了。
所以我们就可以枚举 $i$,来算满足 $lca(u,v) = i$ 的路径的贡献。复杂度为 $\sum_{i=1}^n size_i$,其中 $size_i$ 表示以 $i$ 为根的子树大小。如果原图是链,那么复杂度直接炸到 $O(n^2)$。考虑优化这个过程。考虑换一种顺序来算贡献。假设我们算完了 $i$ 的贡献。我们接下来需要对于每个子树再算贡献。我们可以对每个子树,去算那个子树重心的贡献。然后对于那个子树递归下去。这么说可能有亿点抽象,所以我画了几张图。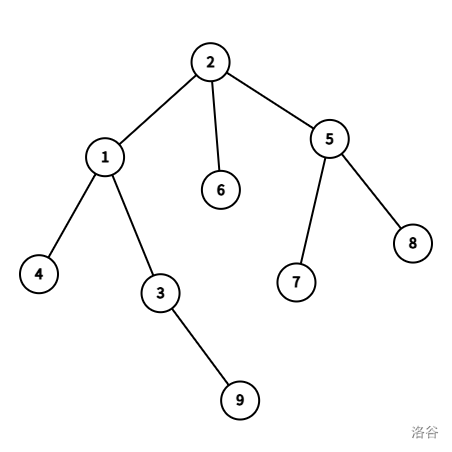
这是一只可爱的树。现在,我们算完了满足 $lca(u,v) = 2$ 的路径的贡献。假设我们现在要算以 1 为根的子树内的贡献。我们找到 1 的子树的重心,也就是 3。我们现在去算 3 的贡献。
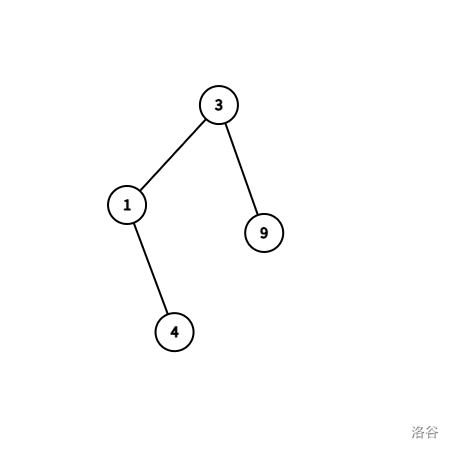
算完 3 的贡献后,我们对这个子树递归下去计算。
但是有入要问了,那这样复杂度不还是 $O(n^2)$ 吗?根据重心的定义,重心的每个子树的大小不超过原树大小的一半。所以递归下去的子树大小小于等于原树的 $\frac{1}{2}$。所以 $T(n)=2T(\frac{n}{2}) + O(n)$。根据主定理,$T(n) = O(n \log n)$。
所以我们就这么算就完事了。代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll Pig = 2e4 + 10;
ll cnt[4], ans, d[Pig], sze[Pig], p[Pig], cur;
set<pair<ll, ll> > g[Pig];
vector<ll> pnt;
//求重心
void dfs1(ll i, ll f) {
pnt.emplace_back(i);
sze[i] = 1;
p[i] = 0;
cnt[d[i] % 3]++;
for (auto j : g[i]) {
if (j.first == f)
continue ;
dfs1(j.first, i);
p[i] = max(p[i], sze[j.first]);
sze[i] += sze[j.first];
}
}
//计算子树答案
void cal(ll i, ll f) {
ans += 2 * cnt[(3 - d[i]) % 3];
for (auto j : g[i]) {
if (j.first == f)
continue ;
d[j.first] = (d[i] + j.second) % 3;
cal(j.first, i);
}
}
//递归下去分治
void dfs2(ll i) {
vector<ll> v;
vector<pair<ll, ll> > v1;
cnt[0] = 1;
cnt[1] = cnt[2] = 0;
for (auto j : g[i]) {
cur = j.first;
d[j.first] = j.second % 3;
pnt.clear();
cal(j.first, i);
dfs1(j.first, i);
for (ll k : pnt) {
p[k] = max(p[k], sze[j.first] - sze[k]);
if (p[k] < p[cur])
cur = k;
}
v.emplace_back(cur);
v1.emplace_back(j);
}
g[i].clear();
for (auto j : v1)
g[j.first].erase(pair<ll, ll>{i, j.second});
for (ll j : v)
dfs2(j);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
ll n;
cin >> n;
for (ll i = 0, u, v, c; i < n - 1; i++) {
cin >> u >> v >> c;
g[u].emplace(v, c);
g[v].emplace(u, c);
}
dfs2(1);
ans += n;
cout << ans / gcd(ans, n * n) << "/" << n * n / gcd(ans, n * n);
return 0;
}
下面是几个更难的例子。
考虑分数规划。设每条边有两个权值 $a_i,b_i$,$a_i$ 就是原树边权,$b_i$ 就是 1。则答案等于 $\frac{\sum_{e \in S} a_i}{\sum_{e \in S} b_i}$。按照套路,进行二分答案。设当前在询问 $x$ 是否合法。check 函数相当于寻找有没有长度在 $L,U$ 之间,且路径上边的权值和非负的路径(注意,这里的权值表示 $a_i - x$)。可以用点分治 + 线段树得到一个 $n\log^3 n$ 的过不去的做法。正解是点分治。假设我们在算 $i$ 的贡献。将每个连通块按照最大深度排序,然后把割掉 $i$ 之后每一个子连通块中的路径按照深度排序,那么随着深度的递增,可以和当前路径匹配的路径的深度区间左右端点是单调递增的,然后用单调队列就可以做到 $n \log^2 n$ 了。
假设所有的点对都在点 i 中。我们只考虑以 i 为中心,送货距离最长的点对。 有以下三种情况:
- 所有点对在同一个子树内。 这种情况的话,显然答案在那个子树中更优。
- 有的点对的路径穿过 i 这种情况答案在 i 更优。
- 所有点对不同一个子树内。 这种情况答案在 i 更优。 所以如果所有点对在同一个子树内,则在那个子树的重心出递归下去进行计算。
习题:P3085
2. 点分树
例题:P6329
距离小于等于 k?不可做!首先单次的询问可以用点分治来搞。但是多次询问呢?让我们来回忆一下,点分治的过程中,我们会先处理 $u$,再处理 $u$ 的每个子树的重心。我们可以将这个处理的过程建成一棵树。如图所示,这是一只树。
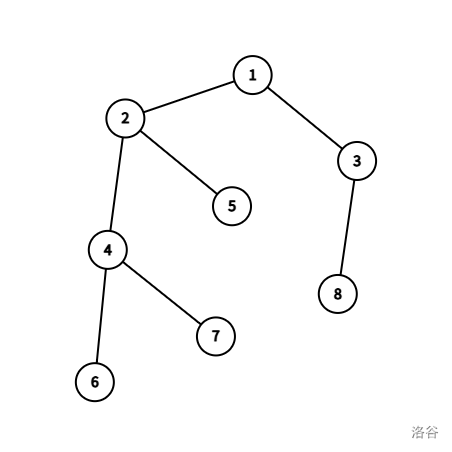
然后这是它的点分树。
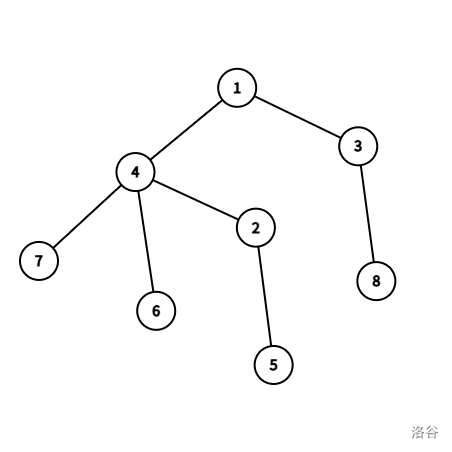
点分树有很多性质:
- 点分树高度不超过 $\log_2 n$
- 点分树的子树对应原树的一个连通块
- 点分树上两点的 $lca$ 一定在原树两点的路径上。
- 点分树上两点的距离不等于原树上两点的距离。(划重点,这里很容易搞混)
性质 1 可以让很多暴力在点分树上有一个优秀的复杂度。回到本题。以刚才那棵树为例。比如说我们要求出到 5 距离小于等于 2 的点个数。那么根据性质 2,我们可以枚举 5 在点分树上的的祖先。比如我们在枚举 4,我们只要求出 $\sum_{lca(u,5) = 4 \land dist(5,4) + dist(4,u) \le k} value_u$。其中 $dist$ 表示两点在原树上的距离。对于 $\sum$ 中的第一条限制 $lca(u,5) = 4$,我们可以先求出满足 $u$ 在 4 的子树内的 $u$ 的 $value$ 和,然后减去满足 $u$ 在 2 的子树内的和,这样就通过容斥算出正确答案了。我们对于每个点维护两颗平衡树,一颗维护 $x$ 的子树内每个点到 $x$ 的距离和 $value$,一颗维护 $x$ 的子树内每个点到 $fa_x$ 的距离和 $value$。这样就可以查询和修改了。复杂度是单次操作 $\log^2 n$ 的。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef int ll;
const ll Pig = 1e5 + 10;
//万恶之源树剖
namespace tree {
ll d[Pig], sze[Pig], fth[Pig], top[Pig], son[Pig], ban[Pig], sze2[Pig], p[Pig];
vector<ll> tr[Pig], pnt;
void add(ll u, ll v) {
tr[u].emplace_back(v);
tr[v].emplace_back(u);
}
void dfs1(ll i, ll f) {
sze[i] = 1;
fth[i] = f;
son[i] = -1;
d[i] = d[f] + 1;
for (ll j : tr[i]) {
if (j == f)
continue;
dfs1(j, i);
sze[i] += sze[j];
if (son[i] == -1 or sze[j] > sze[son[i]])
son[i] = j;
}
}
void dfs2(ll i, ll t) {
top[i] = t;
if (son[i] != -1)
dfs2(son[i], t);
for (ll j : tr[i]) {
if (j == fth[i] or j == son[i])
continue;
dfs2(j, j);
}
}
void init() {
dfs1(1, 0);
dfs2(1, 1);
}
void dfs3(ll i, ll f) {
pnt.emplace_back(i);
sze2[i] = 1;
p[i] = 0;
for (ll j : tr[i]) {
if (ban[j] or j == f)
continue;
dfs3(j, i);
sze2[i] += sze2[j];
p[i] = max(p[i], sze2[j]);
}
}
ll lca(ll u, ll v) {
while (top[u] != top[v]) {
if (d[top[u]] < d[top[v]])
swap(u, v);
u = fth[top[u]];
}
return (d[u] < d[v] ? u : v);
}
ll dis(ll u, ll v) {
return d[u] + d[v] - 2 * d[lca(u, v)];
}
ll get(ll u) {
pnt.clear();
dfs3(u, 0);
//ban[u] = 1;
ll cur = u;
for (ll i : pnt) {
p[i] = max(p[i], sze2[u] - sze2[i]);
if (p[i] < p[cur])
cur = i;
}
return cur;
}
}
ll n, q, root[Pig], root2[Pig], fth[Pig], val[Pig];
//我懒,所以没写平衡树,写了动态开店线段树。
struct node {
ll l, r, sum;
node(ll _v = 0) : sum(_v), l(0), r(0) {}
};
struct segment_tree {
node tr[Pig << 6];
ll cnt = 0;
#define ls(i) (tr[i].l)
#define rs(i) (tr[i].r)
void push_up(ll i) {
tr[i].sum = tr[ls(i)].sum + tr[rs(i)].sum;
}
void upd(ll &i, ll l, ll r, ll x, ll v) {
if (!i)
i = ++cnt;
if (l == r) {
tr[i].sum += v;
return ;
}
ll m = ((l + r) >> 1);
if (x <= m)
upd(ls(i), l, m, x, v);
else
upd(rs(i), m + 1, r, x, v);
push_up(i);
}
ll qry(ll i, ll l, ll r, ll s, ll t) {
if (!i)
return 0;
if (l <= s and t <= r)
return tr[i].sum;
ll ans = 0, m = ((s + t) >> 1);
if (l <= m)
ans += qry(ls(i), l, r, s, m);
if (r > m)
ans += qry(rs(i), l, r, m + 1, t);
return ans;
}
} tr;
//建树
void build(ll i) {
root[i] = ++tr.cnt;
root2[i] = ++tr.cnt;
tree::ban[i] = 1;
for (ll j : tree::tr[i]) {
if (tree::ban[j])
continue;
ll c = tree::get(j);
fth[c] = i;
build(c);
}
}
//查询
ll qry(ll x, ll k) {
ll cur = x, c = 0, ans = 0;
while (cur) {
if (tree::dis(x, cur) > k) {
c = cur;
cur = fth[cur];
continue;
}
ans += tr.qry(root[cur], 0, k - tree::dis(x, cur), 0, n);
if (c)
ans -= tr.qry(root2[c], 0, k - tree::dis(x, cur), 0, n);
c = cur;
cur = fth[cur];
}
return ans;
}
//修改
void chg(ll i, ll k, bool init = 0) {
ll cur = i, c = fth[i];
while (cur) {
tr.upd(root[cur], 0, n, tree::dis(i, cur), k - val[i]);
if (c)
tr.upd(root2[cur], 0, n, tree::dis(i, c), k - val[i]);
cur = fth[cur];
c = fth[c];
}
if (!init)
val[i] = k;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> q;
for (ll i = 1; i <= n; i++)
cin >> val[i];
for (ll i = 1, u, v; i < n; i++) {
cin >> u >> v;
tree::add(u, v);
}
tree::init();
build(tree::get(1));
for (ll i = 1; i <= n; i++)
chg(i, val[i] * 2, 1);
for (ll ans = 0; q; q--) {
ll op, x, y;
cin >> op >> x >> y;
x ^= ans, y ^= ans;
if (op == 0) {
cout << (ans = qry(x, y)) << endl;
} else {
chg(x, y);
}
}
return 0;
}
下面是一个恶心的例子。
每次插入一个点……假如是离线那就可以点分树做,但是在线?我们可以每次暴力加点,但是树的深度会很高。那么,我们既要维护平衡,又要保证结构,还要动态插入。额,什么才能维护呢?这些限制看上去像平衡树,但是不能用 Treap,Splay 这类会改变结构的东西。我们有两种做法。第一种是根号重构。每插入根号个点就将整棵树重构。第二种是用替罪羊树的思想。只要最大深度大于某个值就重构。
习题:P5311
