A： 水题没价值

B： 先设 $\gcd_{i=1}^n a_i = x$，不难发现 $\gcd(x,k) = 1$。所以枚举出 k，然后解个同余方程即可。

C: 水题没价值

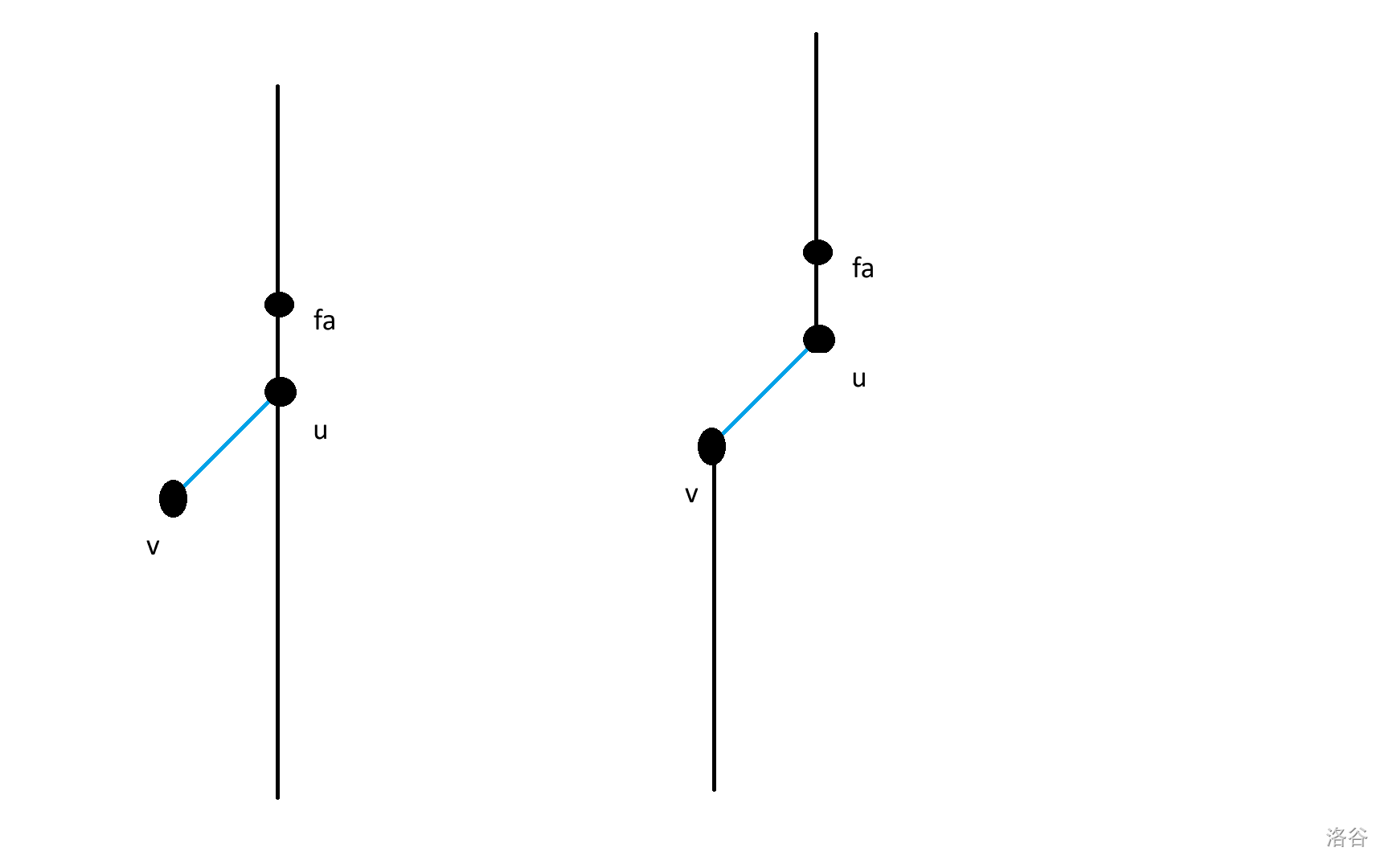
D： 首先，每次操作最多可以将直径增加 1。设树的直径长 $l$。所以操作次数一定大于等于 $n - 1 - l$。现在，我们要尝试构造一组方案，使得每次操作直径都增加 1。注意到如果树上有一条边 $(u,v)$ 满足 u 在某一条直径上，v 不在，则可以进行操作 $fa_u,u,v$，让直径增加一。其中 $fa_u$ 表示以 u 所在的某一条直径的一个端点为根，u 的父亲。

E: 我们直接在每个位置先抛一遍球。这样大部分点都能确定位置了。但是对于 $d_{i+1} = d_{i + 2}$ 的点来说，我们抛球确定不了位置。注意到确定不了的位置一定不挨在一起。所以确定不了的位置的个数小于等于 $\lceil \frac{n}{2} \rceil$ 。在每个确定不了的位置进行 swap 操作，在抛一遍球就可以了。

F： 先鸽着。