已完成 $SA$ 大学习。

$SA$，顾名思义，$Suffix \ Array$，就是后缀数组的意思。

我们先来考虑一个问题。给定一个字符串，多次询问，要我们求出两个后缀的 $\operatorname{lcp}$（最长公共前缀）。

先将字符串的每一个后缀全部插入一颗 $\operatorname{Trie}$ 树。可以发现询问就等价于询问两个后缀对应的点的 $\operatorname{lca}$ 的深度（定义根的深度为 $0$）。

比如字符串 aba。我们构建出其每一个后缀构成的 $\operatorname{Trie}$，其中红色表示这个点代表起始位置为几的后缀。

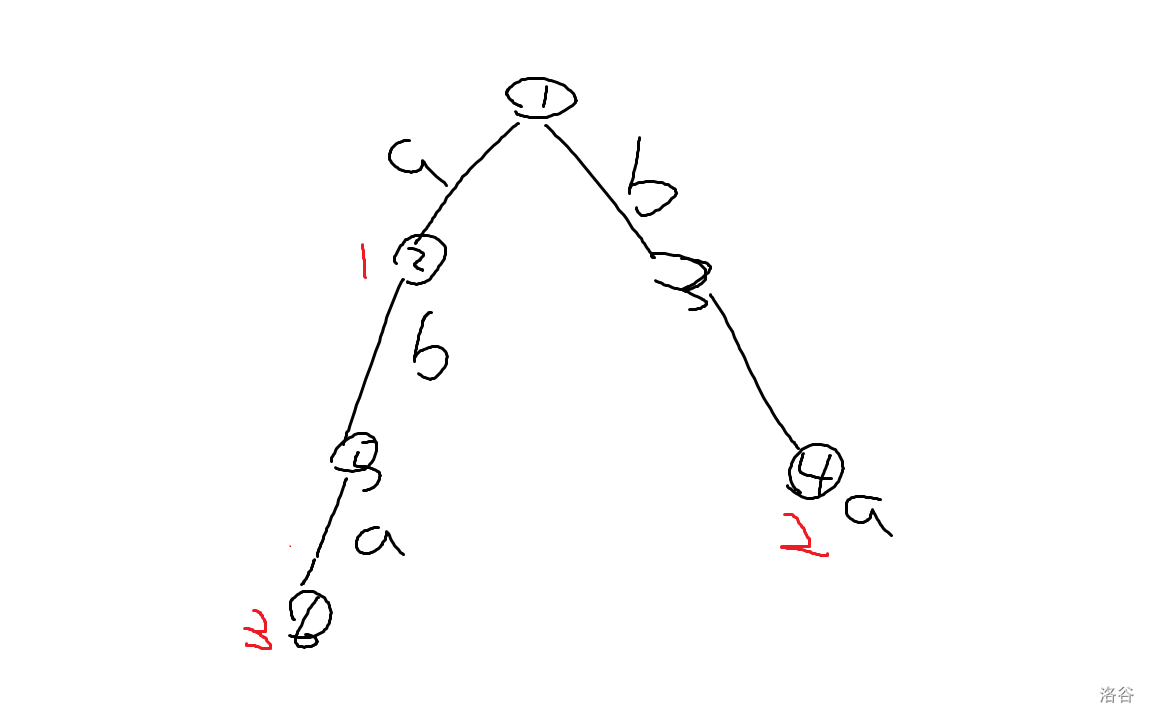
（图画得太好看了，快来夸我）

那么，起始位置为 $3$ 的后缀与起始位置为 $1$ 的后缀的最长公共前缀，就是 $\operatorname{lca}(2, 6)$ 的深度，即为 $1$。

但是，因为我们需要对每一个后缀都插入到 $\operatorname{Trie}$ 里面，所以构建这个 $\operatorname{Trie}$ 树的复杂度是 $O(n^2)$ 的，太慢了。怎么才能优化呢？

尝试优化建树过程。发现这个问题有点像虚树，在这个 $\operatorname{Trie}$ 树上，真正用到的只有所有的叶子和叶子之间的 $\operatorname{lca}$，所以有大量的点没用。我们考虑只记录叶子和他们之间 $\operatorname{lca}$ 的深度。

我们先在 $\operatorname{Trie}$ 树上 $\operatorname{dfs}$，每个点按照边权（连向另一个点的字母）从小到大的顺序来遍历。首先我们注意到，如果我们先对字符串所有后缀排序，那么排序后后缀在 $\operatorname{Trie}$ 上对应的点 $\operatorname{dfn}$ 序一定递增。因为 $\operatorname{Trie}$ 树上每一个点的儿子是按照字符集的大小排序的，所以总会先遍历字典序小的字符，所以 $\operatorname{Trie}$ 树上叶子的 $\operatorname{dfn}$ 的顺序就是后缀的字典序顺序。

那么，我们只需要对所有后缀按照字典序排序，就可以维护出叶子了。但是，我们对后缀排序的复杂度还是 $O(n^2)$ 的。又注意到一个后缀可以从中间被拆分成两端，那么我们可以倍增长度 $len$。定义 $tmp_i$ 表示上一轮的排序结果。每次我们就对 $[i, i + len]$ 排序，排序方法就是将二元组 $(tmp_i, tmp_{i + \frac{len}{2}})$ 按照第一维优先的顺序排序，然后一直倍增直到排序结束。

我们定义 $sa_i$ 表示排名为 $i$ 的后缀的起始位置，$rk_i$ 表示起始位置为 $i$ 的后缀的排名，$sa$ 和 $rk$ 互为逆映射。$end_i$ 表示排名为 $i$ 的后缀在 $\operatorname{Trie}$ 树上对应的点。

让我们回到原来的问题上。我们现在要求出两个点的 $\operatorname{lca}$ 的深度。我们又注意到 $\operatorname{lca}(end_i, end_j)$ 为 ${\operatorname{lca}(end_i, end_{i + 1}), \operatorname{lca}(end_{i + 1}, end_{i + 2}), \cdots, \operatorname{lca}(end_{j - 1}, end_j)}$ 这个集合中深度最小的点。那好办！我们可以求出区间深度最小的点，用 $\operatorname{ST}$ 表即可。

让我们先定义 $dep_i$ 表示 $\operatorname{Trie}$ 树上点 $i$ 的深度，$height_i$ 表示 $dep_{\operatorname{lca}(end_{i - 1}, end_i)}$。那么我们原问题转化为了每次给出 $l, r$，求 $\min_{i \in [rk_l + 1, rk_r]} height_i$。

但是，$height_i$ 还是不好求。

我们仔细观察一下，可以发现有一个性质，就是 $height_{rk_i} \ge height_{rk_{i - 1}} - 1$。

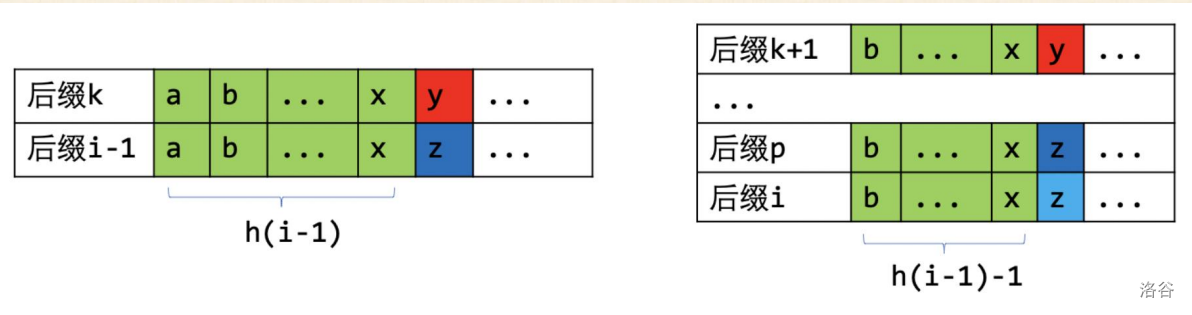
（这张图绝对是我画的）

注意到上一个式子相当于 $i$ 开始的后缀的 $height$ 一定大于等于 $i - 1$ 开始的 $height - 1$。如上面那张图，$i$ 开始的后缀就是 $i - 1$ 开始的后缀删掉前面一个字符。那么 $i$ 的前继后缀一定只比 $i - 1$ 的前继后缀少一个最前面的字符。所以就有了上面那个性质。

那么，我们就可以根据前面那个性质递推求 $height$，复杂度分析一下就是 $O(n)$。

$height$ 数组有很多有趣的性质。让我们来看几道例题。

1. 最小表示法

题意自己看吧。

:::success[Solution] 我们可以把这个字符串复制一遍，然后找到后缀字典序最小的一个，取前 $n$ 个字符就是答案（显然字典序最小的一定至少有 $n$ 个字符）。 :::

2. 两两 lcp

题意：给一个长度为 $N$ 的字符串 $S$，令 $T_i$ 表示它从第 $i$ 个字符开始的后缀。求 $\sum_{1 \le i < j \le N} \operatorname{lcp}(T_i, T_j)$。

:::success[Solution] 首先，这个东西等于 $\sum_{1 \le l < r \le N} \min_{i \in [l + 1, r]} height_i$。那么，我们用笛卡尔树，每个点的值为 $height_i$，按照值小的为父亲。这样最小值为 $height_i$ 的区间个数就是左侧子树大小和右侧子树大小的乘积。 :::

3. 优秀的拆分

题意：寻找字符串中 $AABB$ 式的子串。

:::success[Solution] $AABB$？我们拆成求出以一个点结尾的 $AA$ 的个数 $f$ 和以一个点开始的 $BB$ 串个数 $g$，则答案就是 $\sum_{i = 1}^n f_i g_{i + 1}$。

首先我们有 $g$ 就是反串的 $f$。那么我们只考虑 $g$。首先，我们可以用哈希枚举 $i, j$，判断有没有从 $i$ 开始的 $AA$ 串来求 $f$。考虑最后的 $5$ 分。

我们原本是枚举的点对。现在我们来考虑枚举 $AA$ 串中 $A$ 的长度 $len$，然后每 $len$ 个点设一个关键点。这样，每个长度为 $2len$ 的 $AA$ 串至少经过 $2$ 个关键点。

那么我们就只考虑相邻的关键点，看看多少个 $AA$ 串包含这两个关键点。假设这两个关键点分别为 $a, b$。

我们先分类讨论一下。$PS$：$\operatorname{lcs}$ 就是反串的 $\operatorname{lcp}$。

1. $\operatorname{lcp}(a, b) + \operatorname{lcs}(a, b) < len$ 稍微想想就可以发现这种情况无解。

2. $\operatorname{lcp}(a, b) + \operatorname{lcs}(a, b) \ge len$

   

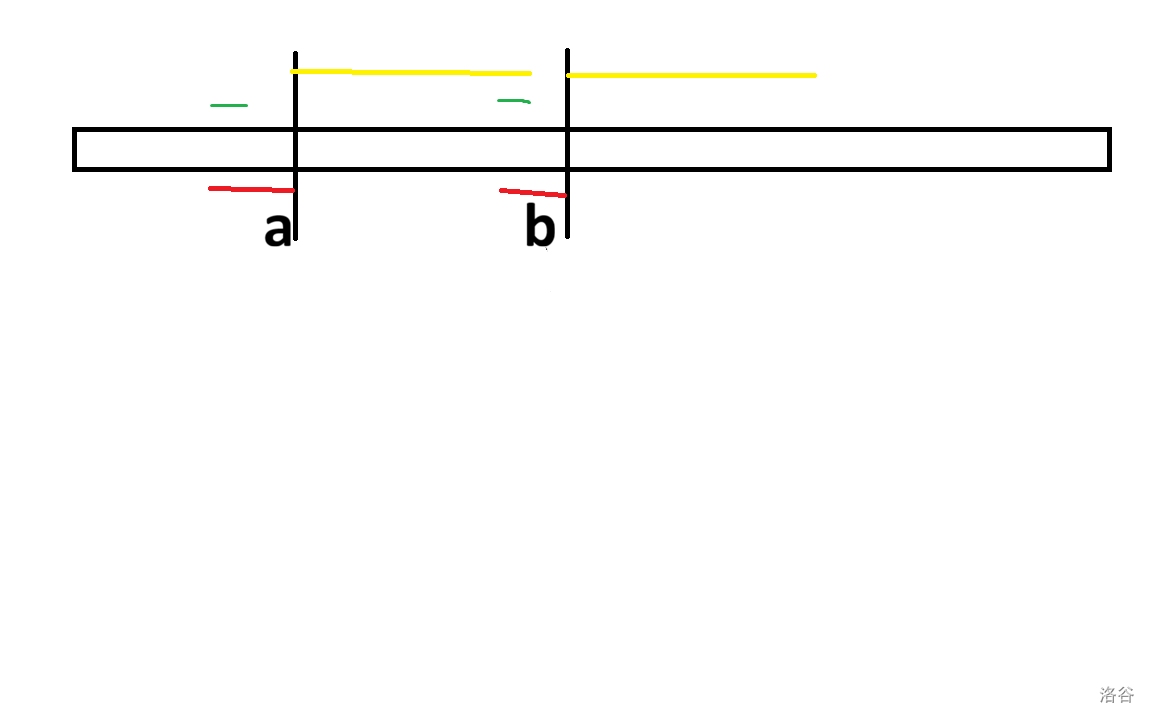
   图中 $a, b$ 表示相邻的两个关键点。然后红色表示 $\operatorname{lcs}$，黄色表示 $\operatorname{lcp}$。然后绿色表示红黄相交的部分。我们注意到从前面的绿色部分的任一点开始，一定存在分界点（$AA$ 串中间的那个点）在第二个绿色点的一个 $AA$ 串。

   那么我们求出绿色部分，用线段树维护一下即可。求出 $\operatorname{lcp}, \operatorname{lcs}$ 就用后缀数组。 :::

4. 跳蚤

题意：把串分成不超过 $k$ 个子串，然后对于每个子串 $S$，从 $S$ 的所有子串中选择字典序最大的那一个，并在选出来的 $k$ 个子串中选择字典序最大的那一个。称其为“魔力串”。现在找一个最优的分法让“魔力串”字典序最小。输出魔力串即可。

:::success[Solution] 首先，预处理出后缀数组之类的东西。我们先尝试二分答案。但是，答案是个字符串二分不了。那怎么搞呢？

我们尝试二分子串的排名来做。那么我们就先需要解决如何根据子串的排名求位置这个问题。这里，我们就需要用到一个结论，一个字符串的本质不同的子串个数等于 $\sum_{i = 1}^n (n - sa_i + 1 - height_i)$。这个式子可以理解为，对 $\operatorname{Trie}$ 树上每一个叶子节点的深度，减去 $\operatorname{dfn}$ 序最大的满足 $\operatorname{dfn}$ 序比当前叶子小的叶子与当前叶子 $\operatorname{lca}$ 的深度。这有点像建虚树，然后求出虚树点数的过程。

那么我们求排名 $k$ 对应的位置的话，就按照排名从小到大枚举后缀，然后比较排名与当前后缀 $i$ 的新贡献 $(n - sa_i + 1 - height_i)$ 的关系。如果排名大，那么排名减去该贡献，继续枚举后缀。否则，字符串的开头、结尾就分别是 $sa_i$ 和 $sa_i + height_i - 1 + k$。

现在考虑如何写 check 函数。我们需要划分，然后让划分出的每一个子串都小于等于当前二分的子串。然后发现可以贪心。我们按照下标从大到小来划分。如果当前下标对应的字符大于二分子串的第一个字符，那么显然没有合法划分方案。否则，我们找到上一个划分点。如果当前下标到上一个划分点构成的子串大于二分的子串，那么必须进行一次划分，从当前下标 $+1$ 到下一个划分点进行一次划分。最后判断划分的次数是否小于等于 $k$ 即可。 :::

5. 小猪猪与字符串

题意：给定 $n$ 个字符串，询问每个字符串有多少子串（不包括空串）是所有 $n$ 个字符串中至少 $k$ 个字符串的子串。

:::success[Solution] 额，在 $k$ 个字符串中出现？$SA$ 很不可做的样子。我们尝试枚举一个字符串的每一个后缀，求出以这个后缀的开头开始的合法前缀的贡献。

先将所有的字符串合并在一起。我们对每一个字符串之间插入互不相同的分隔符，就可以合并所有的字符串，来求后缀数组了。

我们现在先尝试求出所有的包含了至少 $k$ 个字符串的极小排名区间（区间指 $sa$ 数组的区间，极小指没有子区间满足包含 $k$ 个字符串）。这个东西可以用双指针乱搞。

然后求出所有区间后，用线段树维护答案。对于每一个区间，求出其 $\operatorname{lcp}$。这代表该排名区间内的所有后缀，它们长度为 $\operatorname{lcp}$ 的前缀都是满足条件的。我们要对这个排名区间内的所有点，与当前的 $\operatorname{lcp}$ 取 $\max$。最后统计每个字符串所有后缀对应的 $\max$ 值之和即可。 :::